Latent until activated by the correct frequency wavelengh to resonate the cavity.

Viral latency is the ability of a virus to remain dormant within the host cell

A virus receptor can be defined as a host cell surface component recognized by the virus as a gateway to entry into the cell.

Membrane potential is the difference in electric potential between the interior and the exterior of a biological cell.

Cationic liposomes are spherical structures that contain positively charged lipids. Cationic liposomes can vary in size between 40 nm and 500 nm, and they can either have one lipid bilayer (monolamellar) or multiple lipid bilayers (multilamellar).[1] The positive charge of the phospholipids allows cationic liposomes to form complexes with negatively charged nucleic acids (DNA, mRNA, and siRNA) through ionic interactions.

Ionic interactions arise from electrostatic attraction between two groups of opposite charge. ... These interactions do not produce true “bonds,” since there is no sharing of electrons between the groups involved. The groups are pushed together by their “expulsion” from the polar medium.

The dipole consists of two point electric charges of opposite polarity located close together.

An ion-dipole force is an attractive force that results from the electrostatic attraction between an ion and a neutral molecule that has a dipole. Most commonly found in solutions. ... A positive ion (cation) attracts the partially negative end of a neutral polar molecule.

Dipolar or polar molecules are the molecules that posses an electric dipole. The dipoles of some molecules depend on their environment and can change substantially when they are transferred from one medium to another, especially when molecules become ionized in a solvent.

Photoionization is the physical process in which an ion is formed from the interaction of a photon with an atom or molecule.

In some materials, the absorption of a single photon can trigger a chain reaction that produces a large burst of light. The discovery of these photon avalanches in nanostructures opens the way to imaging and sensing applications.

The photon is a type of elementary particle. It is the quantum of the electromagnetic field, including electromagnetic radiation such as light and radio waves and the force carrier for the electromagnetic force. Photons are massless, so they always move at the speed of light in vacuum, 299792458 m/s.

Photon echo is a fundamental tool for the manipulation of electromagnetic fields.

Photon Echo

The signal of the photon echo (PE) is the optical coherent response of a resonant medium (such as a crystal doped with ions) to the effects in certain conditions of two or more laser pulses separated in time.

From: Fundamentals of Femtosecond Optics, 2013

7 Conclusion and Outlook
R-doped crystals fulfill many of the requirements for an efficient QIP system. Protocols exist that take advantage of their specific spectroscopic properties, which can be moreover enhanced and tailored by a number of techniques. In particular, R-doped crystals can provide interfaces between photonic quantum bits, in the optical and microwave ranges, and solid-state qubits. As these qubits can be further processed by optical control, a complete quantum network node could be obtained.

However, a QIP system outperforming a classical system in current information processing tasks is extremely demanding. Still, R-based quantum memories seem much closer to reach the required operating parameters than quantum computers, which are clearly much more complex devices. Strong theoretical and experimental improvements are needed, including development of new materials. Here, bulk single crystals are the preferred choice because of their outstanding spectroscopic properties, although some parameters have still to be improved. Attractive alternatives, like nanostructured materials, may provide additional and important features. In particular, this could allow coupling R ions to other atomic quantum systems, nanoscale quantum mechanical oscillators, or nanocavities.

In such hybrid quantum systems, one could expect to combine efficient processing and storage functionalities, and interface quantum states of different physical nature. This approach may not only benefit QIP but also open the way to fundamental studies in quantum physics.

5.2.2 Crystals
The only Tm3 +-doped crystal system studied so far has been BaY2F8:Tm3 +. In 2004, Patterson et al. reported laser cooling of a Tm3 +-doped crystal for the first time (Patterson et al., 2004). They used a BaY2F8:Tm3 + crystal grown by the Czochralski method and pumped it in single-pass geometry using a high-power OPO with 4–6 W output power in the 1700–2100 nm tuning range to achieve cooling by ~ 1.5 K when pumping at 1902 nm. A second study by Patterson et al. used a high-purity BaY2F8 crystal doped with 1.2% Tm3 + pumped in single-pass geometry (Patterson et al., 2008).

They measured a mean fluorescence wavelength of 1793 nm at room temperature and pointed out the advantageous higher peak absorption cross sections afforded by the crystalline host compared to the amorphous ZBLAN samples studied earlier. The measurement of normalized temperature drop for different pump wavelengths is shown in Fig. 25 and indicates maximum cooling at 1855 nm, where a net temperature drop of 3.2 K was obtained with 4.4 W of pump power. The solid curve shown in Fig. 25 is a fit to the experimental data and yielded a quantum efficiency of η = 0.98 and a background absorption coefficient of 2 × 10− 4 cm− 1. The cooling efficiency was highest with 3.4% at a pump wavelength of 1934 nm.

Ultrafast spin dynamics in the ground state of a rare‐earth‐ion doped crystal are studied by the polarization spectroscopy with the optical pump‐probe technique. Quantum‐ beat FID signals in the subnanosecond region were observed. Their Fourier transform gives the ESR spectra. The spin‐lattice relaxation time T1 is obtained from the decay curve of the optically‐induced magnetization up to the room temperature, where the relaxation time is of the order of picoseconds. The observed temperature dependence of the rate 1/T1 near room temperature deviates from the well‐known T9 dependence. Considering the effect of the Debye temperature of the host crystal on the Raman process, the observed temperature dependence of 1/T1 can be explained well. Ultrafast spin dynamics such as observed in the present work cannot be observed by the conventional ESR, whose time resolution is nanoseconds at best.

Optical Nuclear Polarization
In 1967, Maier and Wolf observed nuclear hyperpolarization in pure anthracene single crystals upon illumination with unpolarized white light. Later the effect was also found in doped crystals of other condensed aromatic compounds. The effect has a maximum at rather low fields (around 0.01 T), although it often remains observable at higher fields. Mostly samples are polarized outside the magnet and, due to long T1, transferred conveniently into the magnet for the NMR measurement.

It has been shown that the origin of the optical nuclear polarization (ONP) is electron hyperpolarization, called optical electron polarization (OEP), occurring in the triplet state.
Upon light excitation, excited electronic singlet states are populated (Scheme 4). Intersystem crossing (ISC) allows for population of electronic triplet states. Owing to zero field splitting (ZFS), in molecules the three triplet electron states are not degenerate.

As pointed out by Wolf and van der Waals in the late 1960s, spin-orbit coupling pathways allowing for ISC are highly spin selective. Therefore, often only one of these three electronic triplet states is populated – the one that has the symmetry matching the preceding excited singlet state. Similarly, the decay to the ground state S0 is controlled by spin-selective ISC. Hence, non-Boltzmann electron population and therefore electron hyperpolarization is created.

This electron hyperpolarization can be transferred to nuclear hyperpolarization by static hyperfine coupling during the lifetime of the triplet state. As shown by both Veeman and Stehlik, the optimum polarization transfer to nuclei can be reached if a selective mixing of the electronic triplet states by a hyperfine interaction occurs, which leads to level anticrossing (LAC) by conserving the total magnetic quantum number. In molecular crystals, migration of triplet excitations and their trapping may control the kinetics and site of the occurrence of ONP.

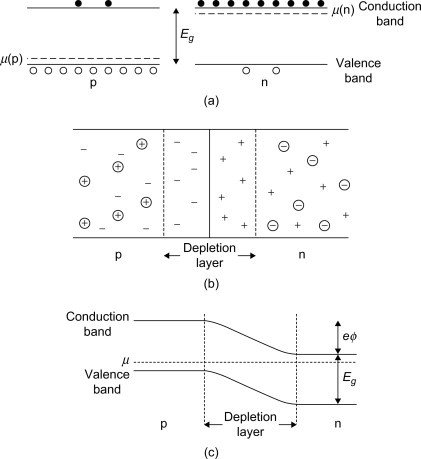
A simple p-n junction is fabricated by taking a single intrinsic semiconductor such as Si in which donor impurities are introduced in one region and acceptor impurities are introduced into another.

It is easier to visualize the p-n junction as equivalent to two Si crystals doped with donor (n-type) and acceptor (p-type) impurities joined together with polished surfaces. In practice, this is not a good idea because the surface effects would interfere with the properties of the semiconductor. These semiconductors have different chemical potentials, respectively. Initially, most of the conduction electrons are at the n-type, and the holes are at the p-type semiconductor.

This scenario is shown in Figure 10.3a. However, when the two materials are joined together, some of the conduction electrons will diffuse to the p-type material while some of the holes will diffuse to the n-type material. When an electron diffuses to the p-type layer, it will recombine with a hole due to the large concentration of holes in that layer. A similar situation will arise when a hole diffuses to the n-type layer. As more and more electrons and holes diffuse to the p- and n-type layers, the number of carriers in the junction will be greatly reduced. Thus, the layer on either side of the junction has much lower concentration of carriers than the rest of the semiconductor. This is known as the depletion layer, which is shown in Figure 10.3b and usually has an approximate length of
Å

We note that the donor and acceptor ions are much too heavy to diffuse like the electrons and holes. Thus, the p-n junction is formed in the semiconductor with a common chemical potential
This is shown in Figure 10.3c.

Figure 10.3. (a) The electrons (solids) and holes (open circles) in p- and n-type semiconductors. (b) When the p- and n-type regions are in contact, there are practically no carriers in the depletion region. The acceptor and donor ions are represented by circles with signs. (c) The distribution of charge at a p-n junction produces a contact potential across the junction.

4 Electrical characterization
Resistivity, magnetoresisitance and Hall effect were measured on β-FeSi2 crystals from room temperature (RT) down to below 20 K. The magnetic field strength was in the range 0.1 to 0.8 T, a standard value was 0.495 T. Ohmic contacts were made by a Pt adhesive. Bridge and van der Pauw configurations were used. Fig. 2 shows the dependence of the resistivity ρ on temperature for undoped crystals and for crystals doped with Cr, Mn, Co and Ni. All the samples revealed semiconducting behaviour. Values of ρ were in the range between 0.2 and nearly 100 Ωcm at RT, and between nearly 100 and 1000 Ωcm at 11 K. We found p-type behaviour in all samples from the sign of the Hall-coefficient.