Nana, Direct Internal connection to God, WWG1WWA, MAGA, Angels are here already #FightLikeGodIsBesideYou
All you have to do is Google or Duckduckgo:
Frequency music sleep
Frequency music God
Frequency music 8 hour
Frequency music healing
Frequency music DNA
Frequency music Love
Pick your desired result.
Dont expect things to happen overnight sometimes it takes a while, the more grounding you do and the more you cleanse your body and pineal gland the more the return.
I also drink no more than 10 oz of tonic water with quinnine per day along with a vitamin regimine.
I heard today that apricot juice is a good cleanser too, gonna try that. No floride! Research cleansing pineal gland & groun
Frequency music and... Quantum Dots?
https://aip.scitation.org/doi/10.1063/1.5126670?af=R&feed=most-recent&
Eigenfrequencies or natural frequencies are certain discrete frequencies at which a system is prone to vibrate. Natural frequencies appear in many types of systems, for example, as standing waves in a musical instrument or in an electrical RLC circuit.
An RLC circuit is an electrical circuit consisting of a resistor, an inductor, and a capacitor, connected in series or in parallel. The name of the circuit is derived from the letters that are used to denote the constituent components of this circuit, where the sequence of the components may vary from RLC.
LCR series circuit is also known as tuned or acceptor circuit. They have many applications particularly for oscillating circuits. Series LCR circuit has applications in radio and communication engineering. They can be used to select a certain narrow range of frequencies from the total spectrum of ambient radiowaves.
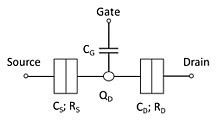
A single-electron transistor (SET) is a sensitive electronic device based on the Coulomb blockade effect. In this device the electrons flow through a tunnel junction between source/drain to a quantum dot (conductive island).
Here we investigate high frequency AC transport through narrow graphene nanoribbons with top-gate potentials that form a localized quantum dot. We show that as a consequence of the finite dwell time of an electron inside the quantum dot (QD), the QD behaves like a classical inductor at sufficiently high frequencies ω ≥ GHz.
When the geometric capacitance of the top-gate and the quantum capacitance of the nanoribbon are accounted for, the admittance of the device behaves like a classical serial RLC circuit with resonant frequencies ω ∼ 100-900 GHz and Q-factors greater than 10(6). These results indicate that graphene nanoribbons can serve as all-electronic ultra-high frequency oscillators and filters, thereby extending the reach of high frequency electronics into new domains.
This chapter discusses three subjects, the quantum capacitance, the size-dependent dielectric function, and the doping of a quantum dot. The main difference in quantum capacitance from its classical definition is the fact that there is no such thing as storage of charge alone and the charge of electron is discrete. The classical capacitance taking into account the discreteness of electronic charge is quite different when there are only few electrons.
Only when the number of electrons is large does the discreteness of electronic charge cease to exhibit new features. When the size is below a couple of nanometers, quantum mechanically the kinetic energy of the stored electrons becomes dominant over the electrostatic stored energy. Pauli's exclusion principle plays an additional role in quantum capacitance.
The size-dependent dielectric function is not defined according to the usual definition, because of the loss of the global nature. It has been emphasized that even the general ɛ(q) is global while ɛ(a), with its boundary condition, is closer to the definition of localized response function. Using a single oscillator placed at the Fermi energy of all the valence electrons without any other adjustable parameter, the calculated value for silicon turns out to be almost identical to ɛ(q = 2π/a), obtained from pseudopotential calculation.
This fact leads to the realization that the pseudopotential calculation is perhaps no more accurate than the single oscillator description for the dielectric constant.
When a voltmeter is used to measure an electronic device, it does not quite measure the pure electric potential (also called Galvani potential). Instead, it measures the electrochemical potential, also called "fermi level difference", which is the total free energy difference per electron, including not only its electric potential energy but also all other forces and influences on the electron (such as the kinetic energy in its wavefunction).
For example, a p-n junction in equilibrium, there is a galvani potential (built-in potential) across the junction, but the "voltage" across it is zero (in the sense that a voltmeter would measure zero voltage).
In a capacitor, there is a relation between charge and voltage, Q=CV. As explained above, we can divide the voltage into two pieces: The galvani potential, and everything else.
In a traditional metal-insulator-metal capacitor, the galvani potential is the only relevant contribution. Therefore, the capacitance can be calculated in a straightforward way using Gauss's law.
However, if one or both of the capacitor plates is a semiconductor, then galvani potential is not necessarily the only important contribution to capacitance. As the capacitor charge increases, the negative plate fills up with electrons, which occupy higher-energy states in the band structure, while the positive plate loses electrons, leaving behind electrons with lower-energy states in the band structure. Therefore, as the capacitor charges or discharges, the voltage changes at a different rate than the galvani potential difference.
In these situations, one cannot calculate capacitance merely by looking at the overall geometry and using Gauss's law. One must also take into account the band-filling / band-emptying effect, related to the density-of-states of the plates. The band-filling / band-emptying effect alters the capacitance, imitating a second capacitance in series. This capacitance is called quantum capacitance, because it is related to the energy of an electron's quantum wavefunction.
Some scientists refer to this same concept as chemical capacitance, because it is related to the electrons' chemical potential.
A dye-sensitized solar cell (DSSC, DSC, DYSC or Grätzel cell) is a low-cost solar cell belonging to the group of thin film solar cells. It is based on a semiconductor formed between a photo-sensitized anode and an electrolyte, a photoelectrochemical system.
In a traditional solid-state semiconductor, a solar cell is made from two doped crystals, one doped with n-type impurities (n-type semiconductor), which add additional free conduction band electrons, and the other doped with p-type impurities (p-type semiconductor), which add additional electron holes.
When placed in contact, some of the electrons in the n-type portion flow into the p-type to "fill in" the missing electrons, also known as electron holes. Eventually enough electrons will flow across the boundary to equalize the Fermi levels of the two materials. The result is a region at the interface, the p-n junction, where charge carriers are depleted and/or accumulated on each side of the interface. In silicon, this transfer of electrons produces a potential barrier of about 0.6 to 0.7 eV.
When placed in the sun, photons of the sunlight can excite electrons on the p-type side of the semiconductor, a process known as photoexcitation.
In silicon, sunlight can provide enough energy to push an electron out of the lower-energy valence band into the higher-energy conduction band. As the name implies, electrons in the conduction band are free to move about the silicon. When a load is placed across the cell as a whole, these electrons will flow out of the p-type side into the n-type side, lose energy while moving through the external circuit, and then flow back into the p-type material where they can once again re-combine with the valence-band hole they left behind. In this way, sunlight creates an electric current.
In the late 1960s it was discovered that illuminated organic dyes can generate electricity at oxide electrodes in electrochemical cells.[9] In an effort to understand and simulate the primary processes in photosynthesis the phenomenon was studied at the University of California at Berkeley with chlorophyll extracted from spinach (bio-mimetic or bionic approach).[10]
On the basis of such experiments electric power generation via the dye sensitization solar cell (DSSC) principle was demonstrated and discussed in 1972.[11] The instability of the dye solar cell was identified as a main challenge. Its efficiency could, during the following two decades, be improved by optimizing the porosity of the electrode prepared from fine oxide powder, but the instability remained a problem.
A modern n-type DSSC, the most common type of DSSC, is composed of a porous layer of titanium dioxide nanoparticles, covered with a molecular dye that absorbs sunlight, like the chlorophyll in green leaves. The titanium dioxide is immersed under an electrolyte solution, above which is a platinum-based catalyst. As in a conventional alkaline battery, an anode (the titanium dioxide) and a cathode (the platinum) are placed on either side of a liquid conductor (the electrolyte).
The working principle for n-type DSSCs can be summarized into a few basic steps. Sunlight passes through the transparent electrode into the dye layer where it can excite electrons that then flow into the conduction band of the n-type semiconductor, typically titanium dioxide. The electrons from titanium dioxide then flow toward the transparent electrode where they are collected for powering a load.