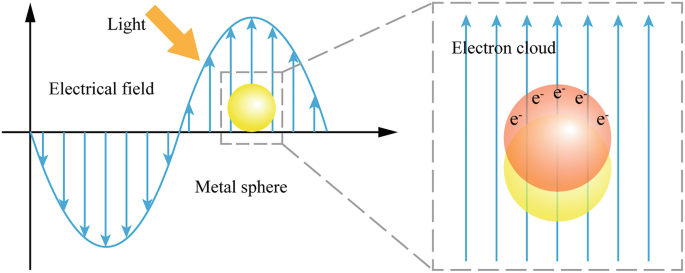
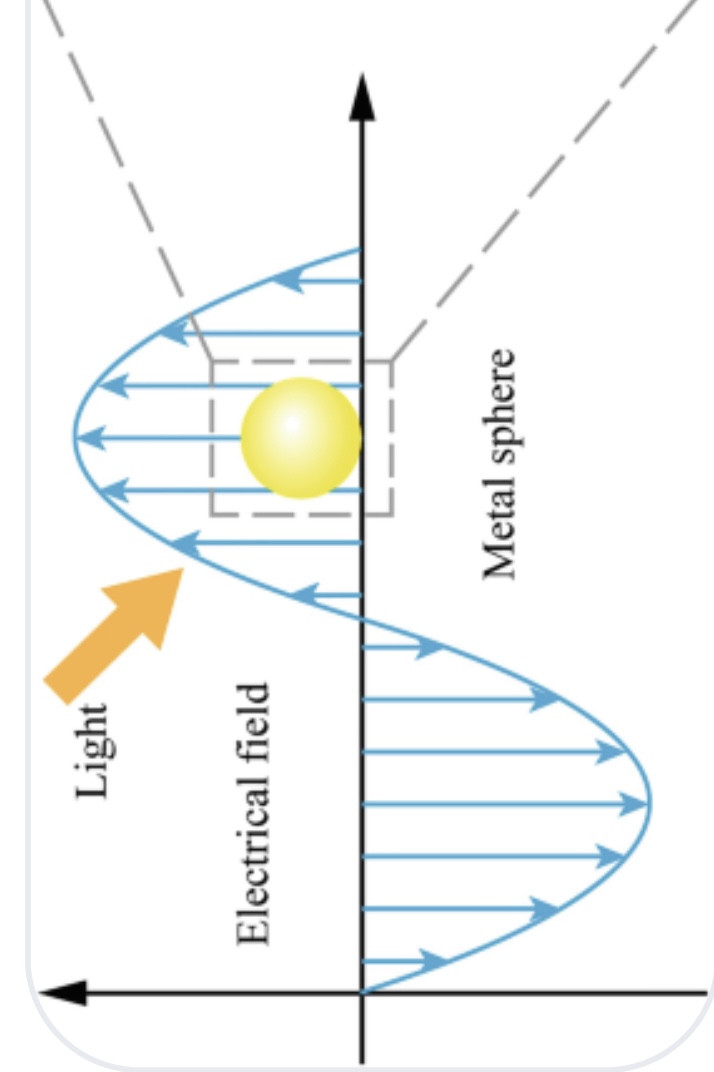
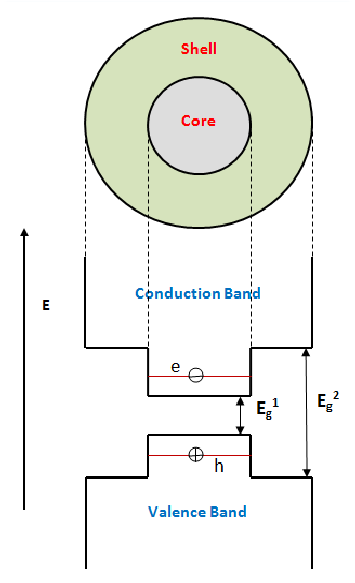
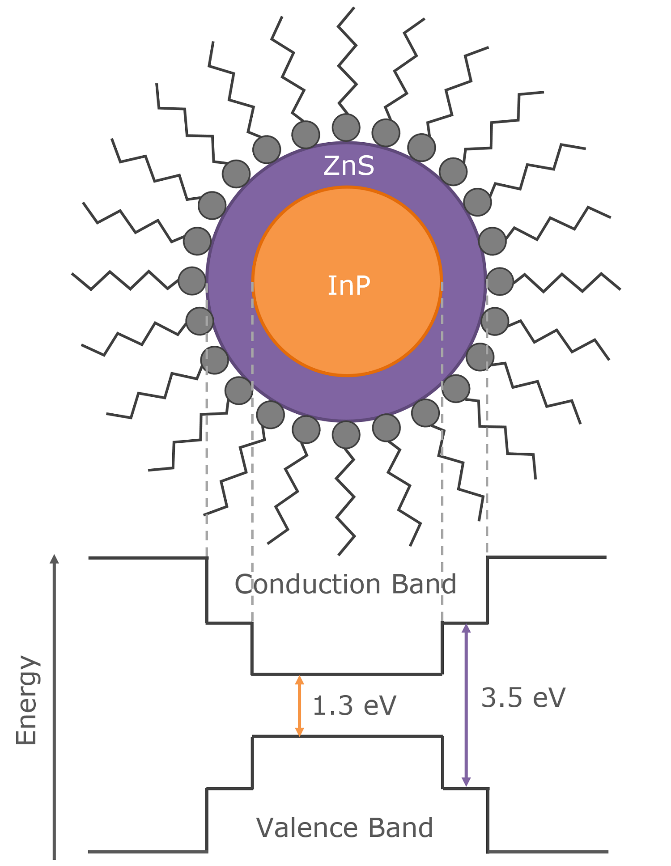
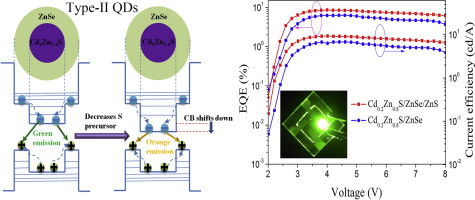
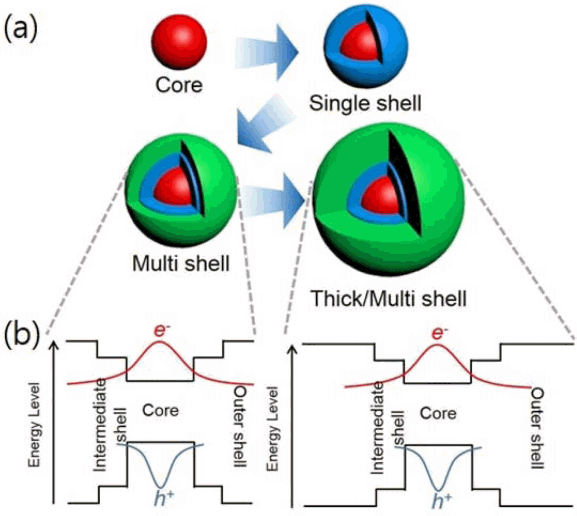
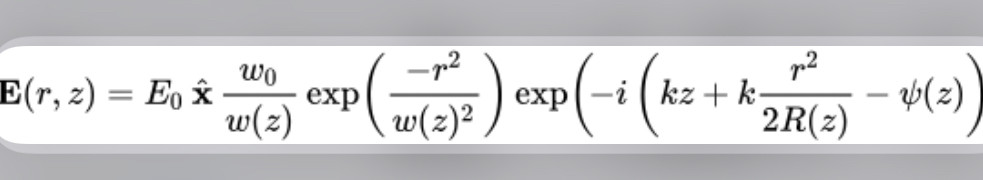So a solid lipid nanoparticle (Pfizer vaccine) can be used as a microlens array for optogenetic stimulation of the brain.
Praying for President Donald J Trump & all those souls dedicating themselves to saving the world from those who seek to destroy us.
🙏 Dear God protect us
Go (D+D) es S
A D D
ADDED TOGETHER
God bless.
Fig. 1 Schematic illustration of the single mode fiber delivered OAM beam. Light is coupled through a single mode fiber and passes through a spiral phase plate at the fiber tip which creates a beam with a helical phase front.
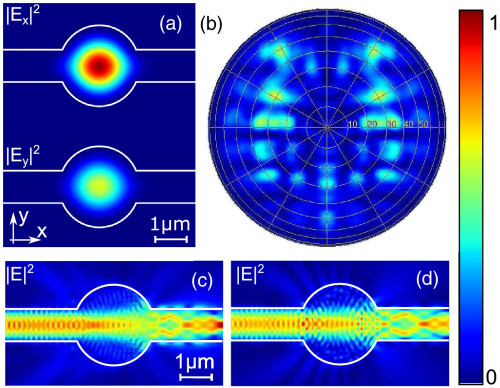
Fig. 1. Simulation of the confined modes in the device for a 2.5 µm diameter cavity and a 0.95 µm waveguide. (a) Intensity of the 𝑥
(𝑦) electric field component for the 𝑥(𝑦)
-polarized confined cavity mode. The two modes, split by 0.05 nm and overlapping by 92%, have different strengths but similar spatial extent. (b) Far-field image of the device with the cavity in the center when pumped from the side, as illustrated in (c) and (d). The far field is on a half-sphere calculated at 1 m distance from the device and is plotted in polar coordinates. The intensity does not match the common intensity scale on the right. The intensity of the total scattered light to the top is less than 10−4. (c), (d) Electric field propagating in the waveguide at the height of the quantum dots, injected on the left into the fundamental eigenmodes of the waveguide; (c) is polarized along the 𝑦
and (d) along 𝑧 direction.
Only followers of this user (@GodsGraciousGift) can see their posts
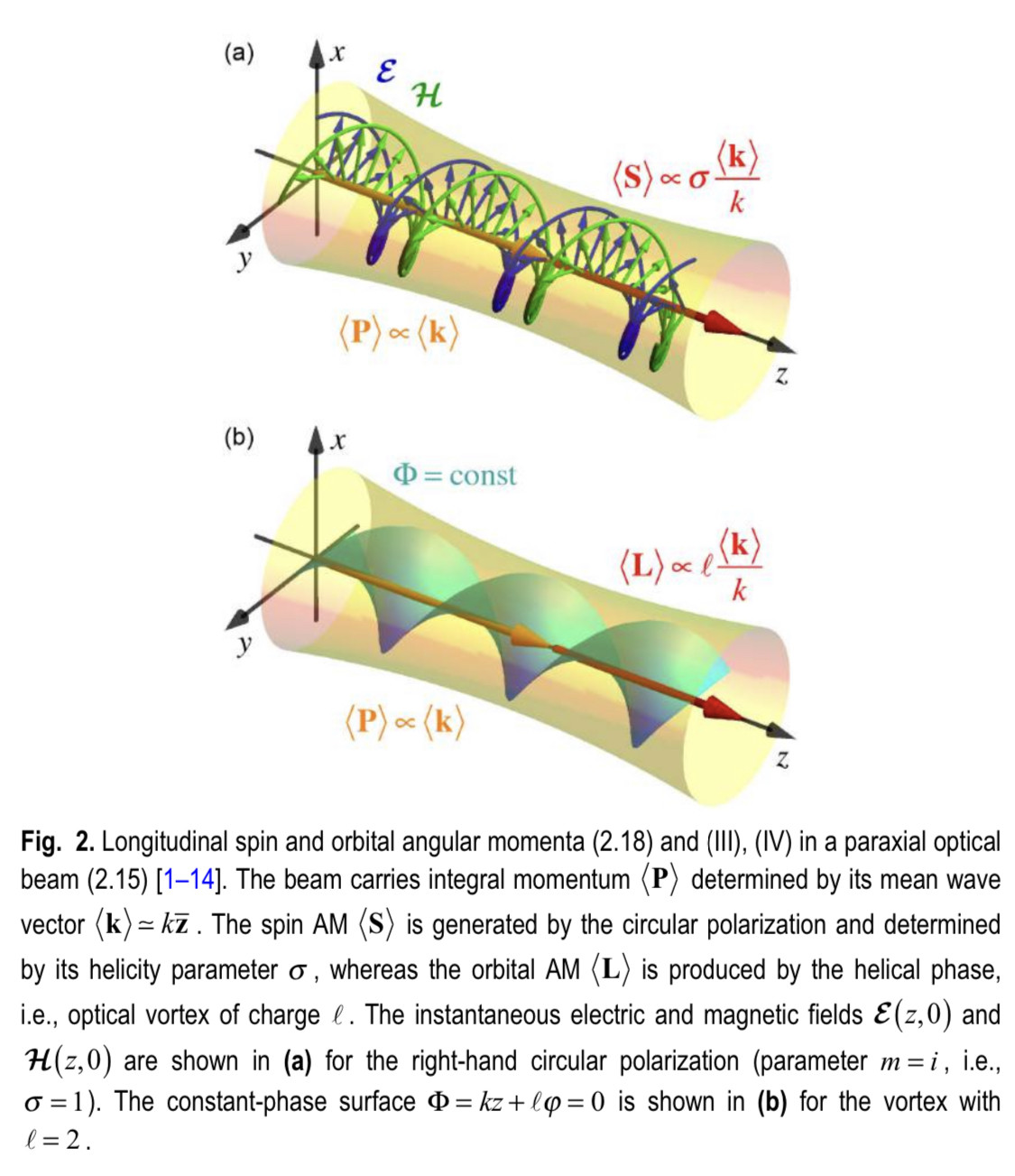
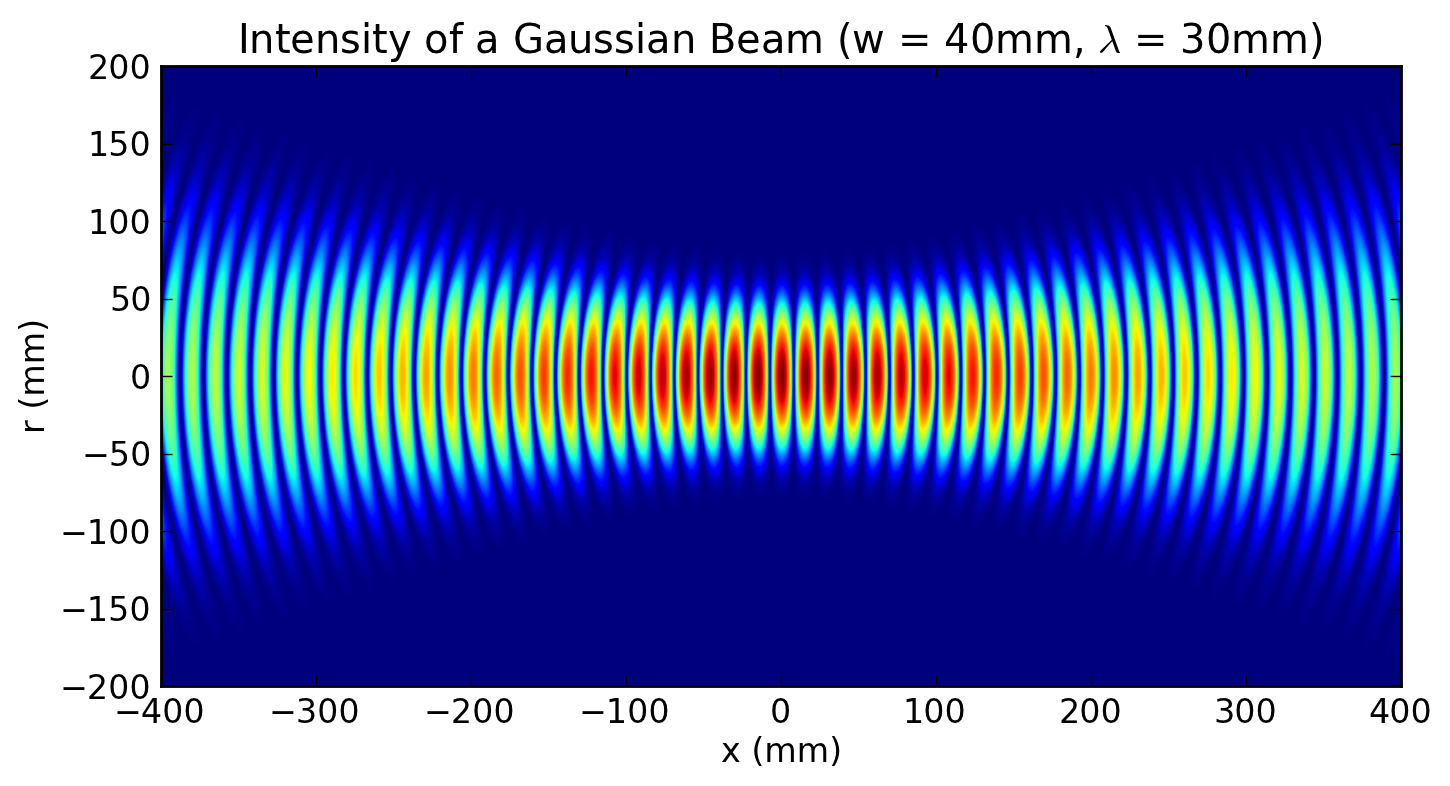
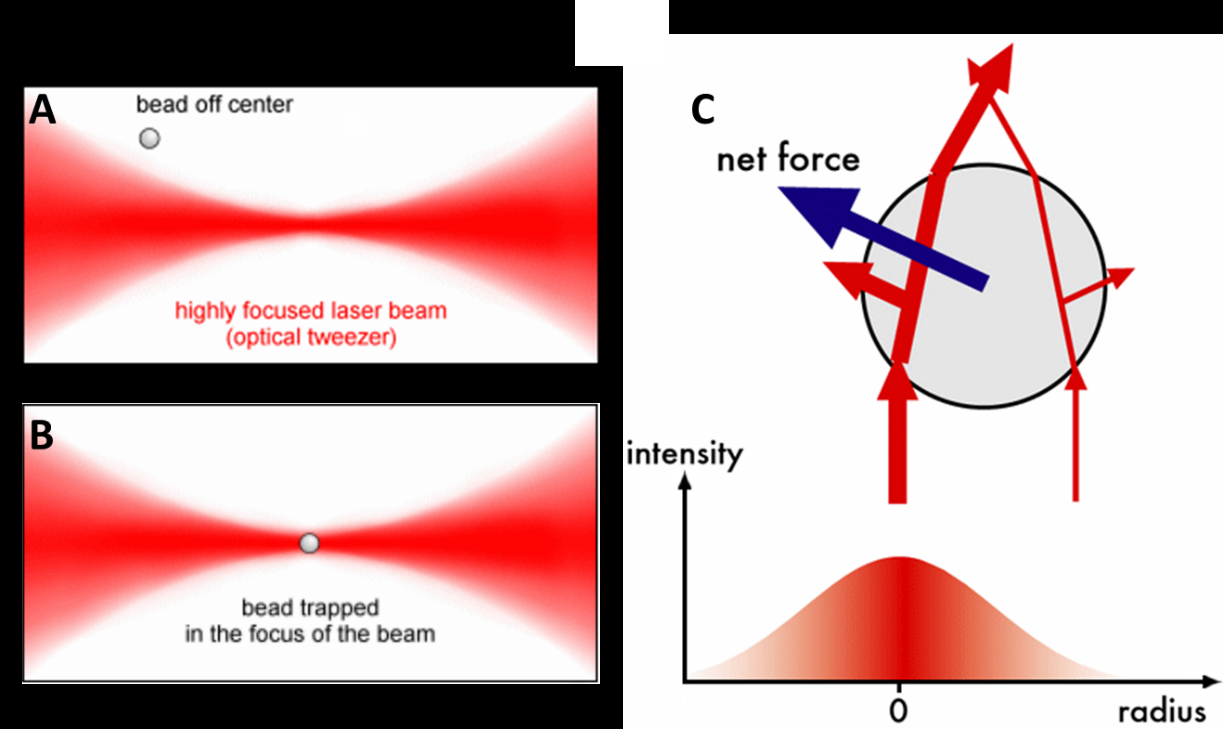
In optics, a Gaussian beam is a beam of electromagnetic radiation with high monochromaticity whose amplitude envelope in the transverse plane is given by a Gaussian function; this also implies a Gaussian intensity (irradiance) profile. This fundamental (or TEM00) transverse Gaussian mode describes the intended output of most (but not all) lasers, as such a beam can be focused into the most concentrated spot. When such a beam is refocused by a lens, the transverse phase dependence is altered; this results in a different Gaussian beam. The electric and magnetic field amplitude profiles along any such circular Gaussian beam (for a given wavelength and polarization) are determined by a single parameter: the so-called waist w0. At any position z relative to the waist (focus) along a beam having a specified w0, the field amplitudes and phases are thereby determined[1] as detailed below.
The Gaussian beam is a transverse electromagnetic (TEM) mode.[4] The mathematical expression for the electric field amplitude is a solution to the paraxial Helmholtz equation.[1] Assuming polarization in the x direction and propagation in the +z direction, the electric field in phasor (complex) notation is given by:
where[1][5]
r is the radial distance from the center axis of the beam,
z is the axial distance from the beam's focus (or "waist"),
i is the imaginary unit,
k = 2πn/λ is the wave number (in radians per meter) for a free-space wavelength λ, and n is the index of refraction of the medium in which the beam propagates,
E0 = E(0, 0), the electric field amplitude (and phase) at the origin (r = 0, z = 0),
w(z) is the radius at which the field amplitudes fall to 1/e of their axial values (i.e., where the intensity values fall to 1/e2 of their axial values), at the plane z along the beam,
w0 = w(0) is the waist radius,
R(z) is the radius of curvature of the beam's wavefronts at z, and
ψ(z) is the Gouy phase at z, an extra phase term beyond that attributable to the phase velocity of light.
The Gaussian function has a 1/e2 diameter (2w as used in the text) about 1.7 times the FWHM.
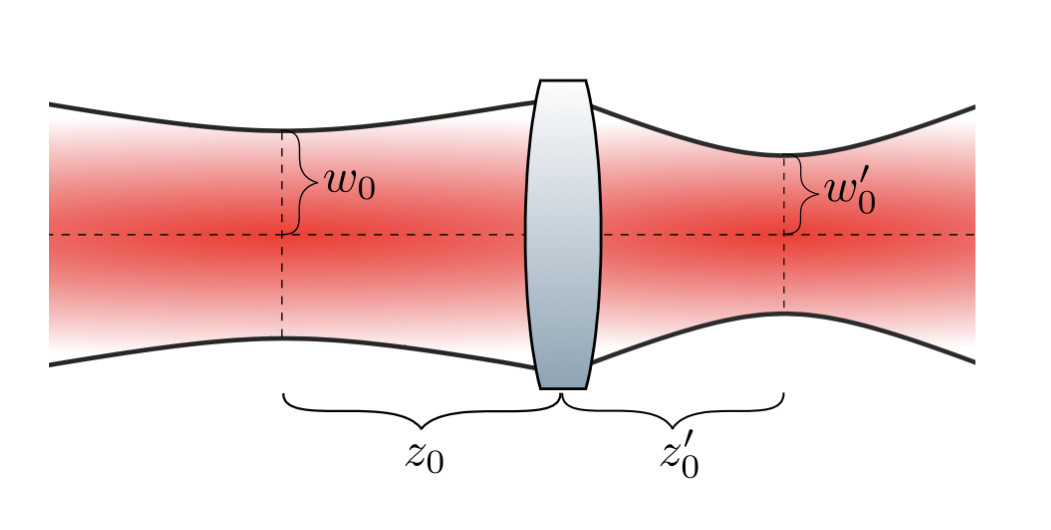
When a gaussian beam propagates through a thin lens, the outgoing beam is also a (different) gaussian beam, provided that the beam travels along the cylindrical symmetry axis of the lens. The focal length of the lens
f
f, the beam waist radius
w
0
w_{0}, and beam waist position
z
0
z_{0} of the incoming beam can be used to determine the beam waist radius
w
0
′
{displaystyle w_{0}'} and position
z
0
′
{displaystyle z_{0}'} of the outgoing beam.
An optical trap is formed by tightly focusing a laser beam with an objective lens of high numerical aperture (NA). A dielectric particle near the focus will experience a force due to the transfer of momentum from the scattering of incident photons.
