What good is a mask unless it is a photomask?

...as the vaccine is activated through the eyes?

Bastards.

woukd ray bans help??

Red glassess???

Blackbody radiation refers to the spectrum of light emitted by any heated object; common examples include the heating element of a toaster and the filament of a light bulb.

A black body or blackbody is an idealized physical body that absorbs all incident electromagnetic radiation, regardless of frequency or angle of incidence. The name "black body" is given because it absorbs all colors of light. A black body also emits black-body radiation.

The quantum annealing process runs, the barrier is raised, and this turns the energy diagram into what is known as a double-well potential (b). Here, the low point of the left valley corresponds to the 0 state, and the low point of the right valley corresponds to the 1 state.

Lattice gauge theory is an essential tool for strongly interacting non-Abelian fields, such as those in quantum chromodynamics where lattice results have been of central importance for several decades. Recent studies suggest that quantum computers could extend the reach of lattice gauge theory in dramatic ways, but the usefulness of quantum annealing hardware for lattice gauge theory has not yet been explored. In this work, we implement SU(2) pure gauge theory on a quantum annealer for lattices comprising a few plaquettes in a row with a periodic boundary condition. These plaquettes are in two spatial dimensions and calculations use the Hamiltonian formulation where time is not discretized. Numerical results are obtained from calculations on D-Wave Advantage hardware for eigenvalues, eigenvectors, vacuum expectation values, and time evolution.

The success of this initial exploration indicates that the quantum annealer might become a useful hardware platform for some aspects of lattice gauge theories.

Quantum annealing starts from a quantum-mechanical superposition of all possible states (candidate states) with equal weights. Then the system evolves following the time-dependent Schrödinger equation, a natural quantum-mechanical evolution of physical systems. The amplitudes of all candidate states keep changing, realizing a quantum parallelism, according to the time-dependent strength of the transverse field, which causes quantum tunneling between states. If the rate of change of the transverse field is slow enough, the system stays close to the ground state of the instantaneous Hamiltonian (also see adiabatic quantum computation).[6]

If the rate of change of the transverse field is accelerated, the system may leave the ground state temporarily but produce a higher likelihood of concluding in the ground state of the final problem Hamiltonian, i.e., diabatic quantum computation.[7][8] The transverse field is finally switched off, and the system is expected to have reached the ground state of the classical Ising model that corresponds to the solution to the original optimization problem. An experimental demonstration of the success of quantum annealing for random magnets was reported immediately after the initial theoretical proposal.[9]

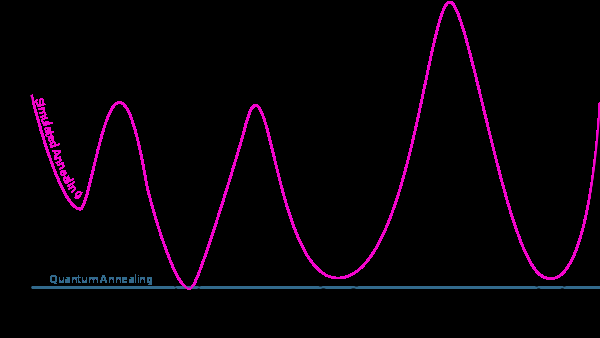
Quantum Annealing (blue line) efficiently traverses energy landscapes by leveraging quantum tunneling to find the global minimum. Quantum annealing offers a significant performance advantage over Simulated Annealing (magenta line), unlocking the potential to solve massive optimization problems previously thought to be impossible.

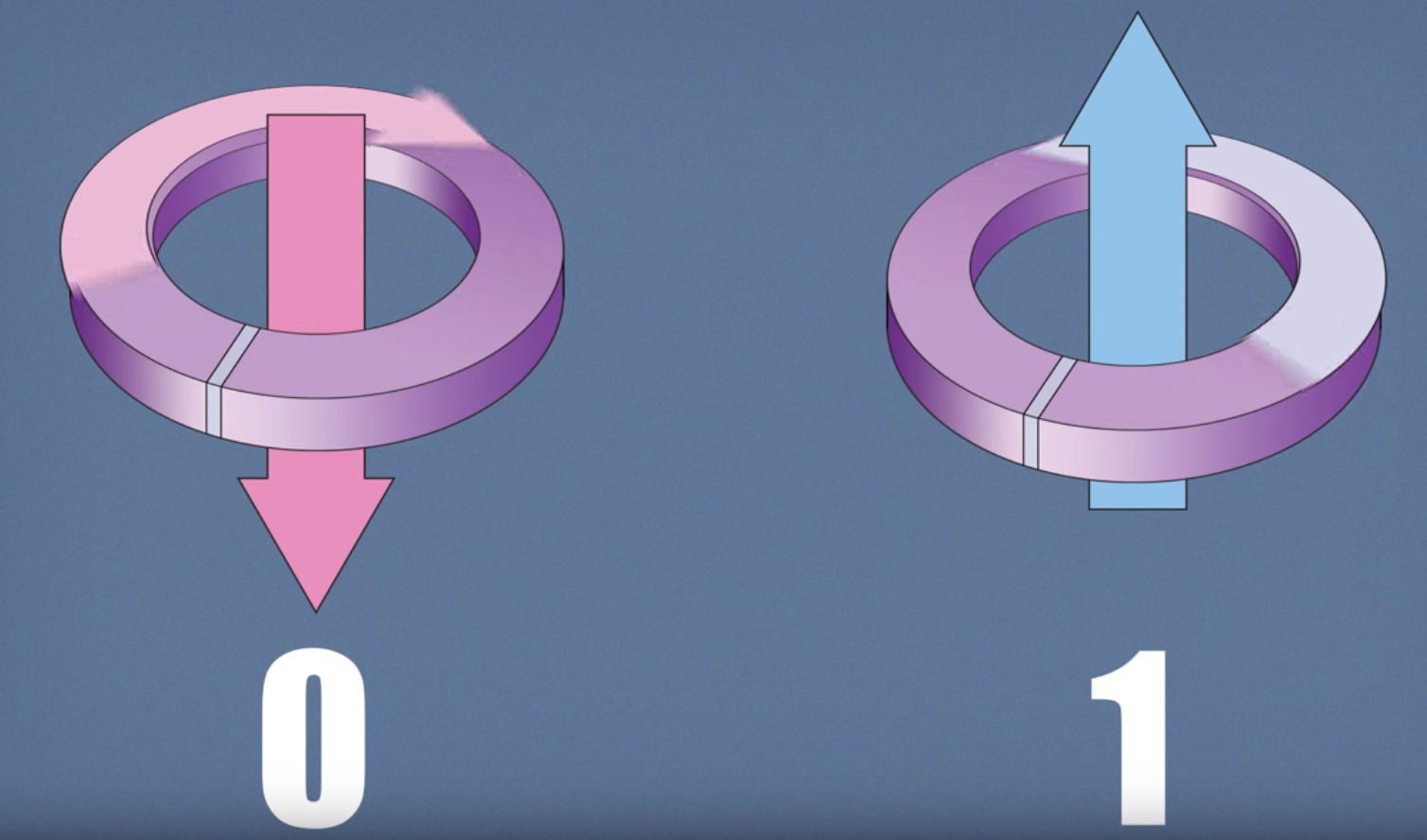
One of the main differences between classical computers and quantum computers is the use of the qubit. The computers we are accustomed to use bits, which is a binary digit that can either have a value of 0 or 1. A qubit can be any two level quantum system, such as a spin in a magnetic field or a single photon. Similar to a bit, a qubit has a possible value of 0 or 1. However, in the quantum world a qubit can be in both states at once (superposition).

The wikipedia definition of quantum superposition states, “any two (or more) quantum states can be added together (“superposed”) and the result will be another valid quantum state; and conversely, that every quantum state can be represented as a sum of two or more other distinct states”. The two states in this definition for the qubit are the 0 or 1 values a normal bit can also have. Basically, before a qubit is observed it is in a superposition of probabilities for 0 and 1. A great example to help explain this is to picture a coin being flipped vs a coin being spun. If you flip a coin it will land on either heads or tails (bit). However, while a coin is spinning you can say the coin’s state is both heads and tails at the same time (qubit). The catch is that once a qubit is observed it will take of the state of either 1 or 0. The video below does a much better job explaining how a qubit works and helps explain superposition.

The thermal radiation of small conducting particles was investigated in the region where the Stephan-Boltzmann law is not valid and strongly overestimates radiation losses. The new criterion for the particle size, at which black body radiation law fails, was formulated. The critical radius rc is expressed through a combination of temperature T and particle conductivity σ: thus rc = c(ћ/2πσkT)1/2. The approach is based on the magnetic particle polarization, which is valid until very small sizes (cluster size) where due to drop of particle conductivity the electric polarization prevails over the magnetic one. It was also shown that the radiation power of clusters, estimated on the basis of the experimental data, is lower than that given by the Stephan-Boltzmann law.